Binary Search Tree
This is a common search tree design. While traversing the tree, if the recursive call is made with a null node as the argument, the value does not exist in the tree. A null node also means that at that location in the tree,
you could insert a new node if that is your intent.
The strategy is to divide your search tree in every recursive call so that your algorithm does not spend time searching through nodes that it already knows cannot possibly contain the
search target.
In other words, if we know that the search target value is less than the parent value of a given node, there is no point in searching to the right of that parent. If we know that
the search target is greater than the parent of a node, then there is no point in searching to the left of that parent.
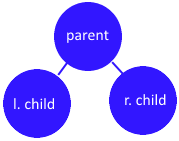
I always picture a node like this:
using System;
public class Node
{
public int Value { get; set; }
public Node Left { get; set; }
public Node Right { get; set; }
public Node(int value, Node left, Node right)
{
Value = value;
Left = left;
Right = right;
}
}
public class BinarySearchTree
{
public static bool Contains(Node root, int value)
{
// when a null node is passed to this method, we have searched all
// possible nodes and could not find the target
if(root == null)
{
return false;
}
else if (root.Value == value)
{
Console.WriteLine("Found target: " + root.Value);
return true;
}
else if (value < root.Value)
{
Console.WriteLine("Less than parent value, going left");
return Contains(root.Left, value);
}
else
{
Console.WriteLine("Greater than parent value, going right");
return Contains(root.Right, value);
}
return false;
}
public static void Main(string[] args)
{
Node n1 = new Node(1, null, null);
Node n3 = new Node(3, null, null);
Node n2 = new Node(2, n1, n3);
Console.WriteLine(BinarySearchTree.Contains(n2, 3));
}
}